数据结构：线性表（2）

顺序存储：

以元素在计算机内的“物理位置”相邻来表示线性表中的数据元素的逻辑关系。
并以表中第一个元素的存储位置作为线性表的基地址。

LOC(ai ) = LOC(ai-1 ) + C
LOC(ai ) = LOC(a1 ) + (i-1)×C

线性表顺序存储结构的特点

1.逻辑上相邻的元素，其物理位置也相邻；
2.可随机存取表中任一元素；
3.必须按最大可能长度预分存储空间，存储空间利用率低，表的容量难以扩充，是一种静态存储结构；
4.插入删除时，需移动大量元素，平均移动元素为n/2。

操作：

插入:

Status listinsert (List &L,int i,ElenType e)
{
	if (i<1||i>L.lenght) return error;
	if (L.lenght>=L.maxsize)
	{
		newbase=(ElemType*)realloc(sizeof(maxsize+newsize)*sizeof(ElemType));
		if (!newbase) exit(1);
		L.elem=newbase;
		L.maxsixe+=newsize;
	}
	q=&L.elem[i-1];
	for(p=L.elem[L.lenght-1];p>q;p--) *(p+1)=*p;
	*q=e;
	L.Lenght++;
	return ok

}

删除同插入类似，不再赘诉。

顺序表的插入和删除都无疑要移动大部分元素，平均情况下要移动表中一半的元素，导致效率低下。

合并：

合并操作有两种算法，在此给出作者认为更好的一种。

void MergeList(list la,list lb,list& lc)

{
	pa=la.elem;
	pb=la.elem;
	lc.maxsize=lc.lenght=la.lenght+lb.lenght;
	pc=lc.elem=(ElemType*)malloc(sizeof(ElemType)*lc.naxsize);
	if (!pc) exit(1);
	pa_last=pa+la.lenght-1;
	pb_last=pb+lb.lenght-1;
	while(pa<pa_last&&pb<pb_last)
	{
		if(*pa<*pb) *pc=*pa;
		else *pc=*pb;
	}
	while(pa<pa_last) *(pc++)=*(pa++);
	while(pb<pb_last) *(pc++)=*(pb++);
}

链式存储：

链式存储的元素都包括一个数据域和一个指针域。

每个数据元素ai与其直接后继数据元素ai+1之间的逻辑关系，数据元素ai除了存储其本身的信息之外，还需存储一个指示其直接后继的信息。

链表中结点在内存中存放的位置可以是不连续的，甚至是零散分布的。

带“头结点”的单链表
在第一个结点之前附加一个“头结点”，令该结点中指针域的指针指向第一个元素结点，并令头指针指向头结点

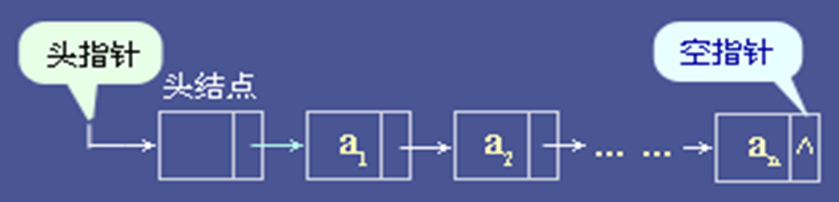
若线性表为空，在不带头结点的情况下，头指针为空(NULL)，但在带头结点的情况下，链表的头指针不为空，而是其头结点中指针域的指针为空。

操作：

销毁：

void DestroyList(Linklist L)
{// 销毁以L为头指针的单链表，释放链表中所有结点空间　
	while (L)
	{
		p = L;
		L = L->next;
		free(p);
	}
	L = NULL;
}

插入：

Status ListInsert (List& l,int i,ElemType e)
{
	p=l;
	j=0;
	while(p&&j<i-1)
	{
		p=p->next;
		j++;
	}
	if(!p||j>i-1) return error;
	s=(list*)malloc(sixeof(lnode));
	s->next=p->next;
	p->next=s;
	s->data=e;
	return ok
}

删除：

Status ListDelete(list& l,int i,ElemType e)
{
	p=l;
	j=0;
	while(!p&&j<i-1)
	{
		p=p->next;
		j++;
	}
	if(!(p->next)||j>i-1)
	{
		return error;
	}
	q=p->next;
	p->next=q->next;
	e=q->data;
	free(q);
	return ok;
}

合并：

void mergelist(list& la,list& lb,list& lc)
{
	pa=la->next;
	pb=la->next;
	lc=pc=pa;
	while(pa&pb)
	{
		if(pa->data<pb->data)
		{
			pc->next=pa;
			pc=pa;
			pa=pa->next;
		}
		else
		{
			pc->next=pb;
			pc=pb;
			pb=pb->next;
		}
		pc=pa?pa:pb;
		free(fb);
	}
}