谱聚类再探

本文最后更新于 2024年6月7日 下午

首先查阅相关的资料，比较谱聚类算法与传统的聚类算法K-mean的区别。

K-mean

K-mean实现：

  1. 确定K值，随机选取K个点
  2. 以这K个点为中心质点，对原始数据集中中的每个点分别计算离哪个中心点更近
  3. 计算结束就将原始数据集分为K个类，对K个类重新计算中心质点（平均值法）
  4. 若全部K类新计算出的中心质点与该类上一个中心质点的距离小于一个阈值，则认为聚类操作已经收敛了，聚类结束
  5. 否则重复步骤2-4

K-mean的优缺点主要如下：

  • 优点：
    1. 原理简单，易于理解
    2. 聚类效果不错
  • 缺点：
    1. 需要提前确定K值（划分种类数）
    2. 个别噪点对于总体效果影响较大

Spectral Clustering

需要先了解：

  1. 邻接矩阵W：衡量两个点之间关系（比如位置上接近，表示两个点关联紧密）的一个矩阵，常有很多的衡量方法。
  2. 度矩阵D：是一个对角矩阵，对角线上每一行元素的值为邻接矩阵W中每行元素值的和。
  3. 拉普拉斯矩阵L：该矩阵具有很多的性质，谱聚类算法与这些性质密切相关
    1. 拉普拉斯矩阵是一个半正定矩阵
    2. 对于任何向量L下列式子成立image20200630114848909.png

主要思想：

如果有A和B两个子图，两个子图间的联系是不是可以用下面这种方式来表示呢？

[公式]

我们只要使上面的式子最小化，是不是就可以保证两个子图联系最小，就可以认为这是两个不相关的部分。

但是如果单纯依靠这种方式，会导致倾向于将孤立的点切开，因为单独一个点到其他部分的权值肯定是最小的。怎么避免这种问题出现呢？有两种办法：

  • 一是将最小化目标改成如下：

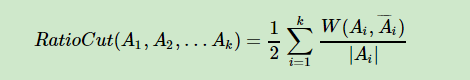
    image20200630121230220.png

  • 而是将最小化目标改为：

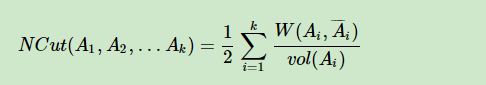
    image20200630121326983.png

这也就引出了谱聚类的两种常用方法。

但是怎么最小化这个值呢？

我们以第一个RdtioCut为例。大神们发现，可以引入一个向量 $h_j (1<=j<=k)$ ，这个向量表示的是什么呢？

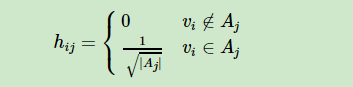
image20200630121735543.png

向量 $h_j$中的每个值 $h_{ij} (1<=i<=n)$ 有两种取值，表示坐标点 $i$ 是不是属于子图 $A_j$ ，$|A_j|$ 表示子图中节点数量

对这个向量进行如下的运算：

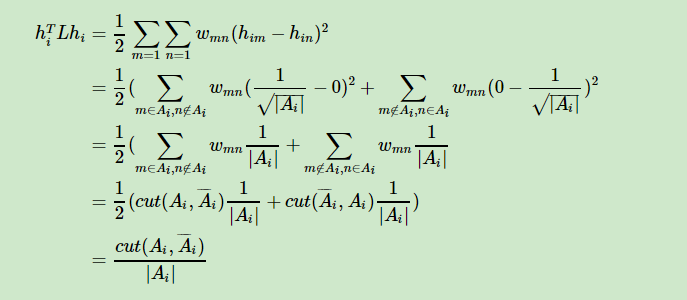
image20200322223247236.png

我们会惊奇的发现这不就是我们最小化的目标吗？只不过现在图中的点只分为了两部分（属于$A_i$ 和不属于）

如果我们想将图分为更多的子图，那么我们的目标就成为了：划分K个子图，每个子图和子图以外部分的连接权重和最小。也即使如下公式最小：

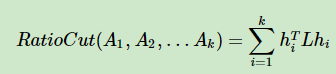
image20200630123607324.png

我们还知道向量 $h_i$和$h_j$是表示点划分的两种情况，$h_i$表示属于$A_i$的点，$h_j$表示属于$A_j$的点。那么这两个向量就应该是正交的。并且 $ h^T h = 1 $。这时我们引入瑞丽商的性质：

  • 当 $h_i^T * h_i=1 $
  • $h_i^T L h_i$等于L的特征值

也就意味着我们最小化的目标变为了求：$H^T L H (H={h_1,h_2…h_k})$ 这个式子最小的k个特征值，他们对应的就是划分最准确的情况。但还有一个问题，我们得到了最小的K个特征值和他们对应的特征向量，怎能才能利用他们聚类呢？其实，我们可以把所得特征值向量对每个样本的表示看作是一种类别编码，我们通过传统聚类的方法能够得到最终结果。

另外

对于Ncut稍不同于上面的RatioCut。因为Ncut中，虽然也引入了一个向量$h_i$，但是向量定义为如下，$vol(A_j)$ 表示的是子图中节点度的和。

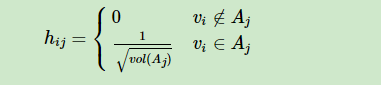
image20200630125353234.png

然后步骤都类似于RatioCut只不过在利用瑞丽商的时候出现了问题，因为 $ h^T h = 1 $并不成立了。所以需要采取一些办法，根据

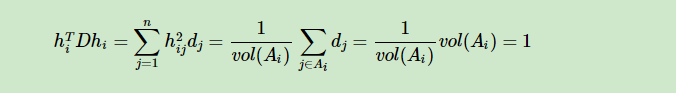
image20200322222411822.png

$m_i^T m_i=1 $

$m_i=D^{1/2}*h_i$

我们需要把现在的 $h_i$ 变成 $m_i$

也即 $h_i^T L h_i = m_i^T * D^{-1/2} * L * D^{-1/2} * m_i =h_i^T * D^{1/2} * D^{-1/2} * L * D^{-1/2} * D^{1/2} * h_i$

此时要求特征值的矩阵变为： $D^{-1/2} * L * D^{-1/2}$

谱聚类实现步骤：

  1. 定义邻接矩阵W
    • ε 近邻法
      • 只取距离小于ε的边，否则为0
    • K 近邻法
      • 两点互为K近邻，否则为0
      • 其一为K近邻，否则为0
    • 全连接法
      • 常采用高斯核函数的方法，每两个点之间的权值都不为0
  2. 度矩阵 D
    • 可根据邻接矩阵W得
  3. 拉普拉斯矩阵矩阵 L
    • $L= D - W$
  4. 正规化
    • $D^{-1/2} L D^{-1/2}$
  5. 计算特征向量
    • 计算K个最小特征值对应的特征向量$h_i$,特征向量组成矩阵$H^{n*k}$
  6. H标准化
    • 消除奇异值带来的影响

以上是谱聚类第一大部分，降维

  1. H使用K-mean进行最后的聚类
    • 得出结果

这是谱聚类的第二大部分，聚类

NCut 推导细节

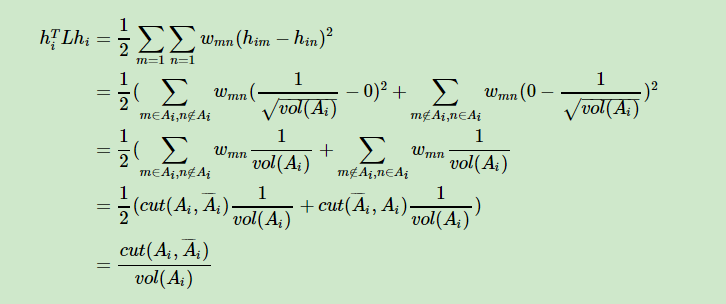
image20200322223222295.png

RadioCut推导细节

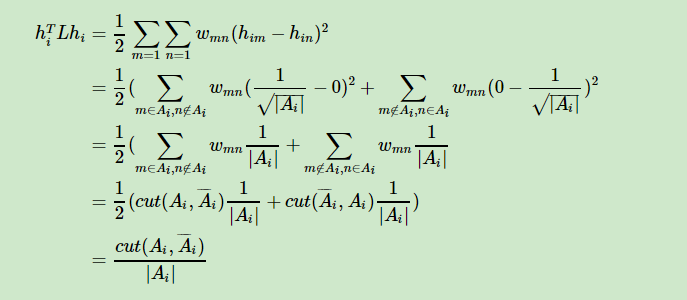
image20200322223247236.png

谱聚类优势

  • 效果好
  • 由于采用了降维的思想，处理高维数据时有优势

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
# coding=utf-8
import math
import random

import matplotlib.pyplot as plt
import numpy as np
import PIL.Image as image
import scipy.io as sio
from sklearn.cluster import KMeans


def loadIMG(filePath):
    img = image.open(filePath)  # 返回图片的像素值

    img = img.convert("RGB")
    m, n = img.size  # 返回图片的大小

    img_vector = np.array(img)

    pixel_vector = []

    for i in range(n):
        for j in range(m):
            if(img_vector[i][j][0] < 150 and img_vector[i][j][1] < 150 and img_vector[i][j][2] < 150):

                pixel_vector.append(np.array([j, i]))

    return pixel_vector


def loaddata():
    # 读取数据
    file = 'GaussianData.mat'
    # 文件名
    file = 'ringData.mat'
    data = sio.loadmat(file)
    matrix = np.array(data['Dataset'])
    return matrix


def distanceRgb(p1, p2):
    r1, g1, b1 = p1[0], p2[1], p2[2]
    r2, g2, b2 = p2[0], p2[1], p2[2]
    rmean = (r1+r2)/2
    r = r1-r2
    g = g1-g2
    b = b1-b2
    return math.sqrt((2+rmean)*(r**2)+4*(g**2)+(2+(255/256-rmean))*(b**2))


def distance(p1, p2):
    # 欧式距离
    return np.linalg.norm(p1-p2)


def getWbyKNN(data, k):
    # data:点阵坐标信息
    points_num = len(data)
    # 点数量：300
    dis_matrix = np.zeros((points_num, points_num))
    # 创建矩阵300*300
    W = np.zeros((points_num, points_num))
    # 创建矩阵300*300
    for i in range(points_num):
        for j in range(i+1, points_num):
            dis_matrix[i][j] = dis_matrix[j][i] = distance(data[i], data[j])
    # 将每个点与其他点的相似度表示成矩阵
    for idx, each in enumerate(dis_matrix):
        index_array = np.argsort(each)
        # 排序
        W[idx][index_array[1:k+1]] = 1
        # 找出距离第idx个点距离最近的k个点
        # 距离最短的是自己，所以取1到k+1
    tmp_W = np.transpose(W)
    # 转置
    W = (tmp_W+W)/2
    # 转置相加除以2是为了让矩阵对称
    return W


def getD(W):
    # 获得度矩阵
    points_num = len(W)
    D = np.diag(np.zeros(points_num))
    # 转换成对角阵
    for i in range(points_num):

        D[i][i] = sum(W[i])
    return D


def getEigVec(L, cluster_num):
    # 从拉普拉斯矩阵获得特征矩阵
    eigval, eigvec = np.linalg.eig(L)
    # 特征值、特征向量
    lenght = len(eigval)
    dictEigval = dict(zip(eigval, range(0, lenght)))
    kEig = np.sort(eigval)[0:cluster_num]
    # 排序
    ix = [dictEigval[k] for k in kEig]

    return eigval[ix], eigvec[:, ix]
    # 取特征值和对应的列向量


def randRGB():
    # 添加颜色，便于区分
    return (random.randint(0, 255)/255.0,
            random.randint(0, 255)/255.0,
            random.randint(0, 255)/255.0)


def plot(matrix, C, k):
    colors = []
    for i in range(k):
        colors.append(randRGB())
    for idx, value in enumerate(C):
        try:
            plt.plot(matrix[idx][0], matrix[idx][1],
                     'o', color=colors[int(C[idx])])
        except:
            pass
    plt.show()


if __name__ == '__main__':
    pixel_vector = loadIMG("./test.jpg")
    # print(pixel_vector)
    cluster_num = 2
    KNN_k = 15
    data = loaddata()
    W = getWbyKNN(pixel_vector, KNN_k)
    # 相似度矩阵
    D = getD(W)
    # 度矩阵
    L = D-W
    # 拉普拉斯矩阵
    eigval, eigvec = getEigVec(L, cluster_num)

    clf = KMeans(n_clusters=cluster_num)
    # 新建类对象
    print(eigvec.real)
    s = clf.fit(eigvec.real)
    # 开始聚类
    plot(pixel_vector, s.labels_, cluster_num)

效果

原图：
test.jpg

聚类后：

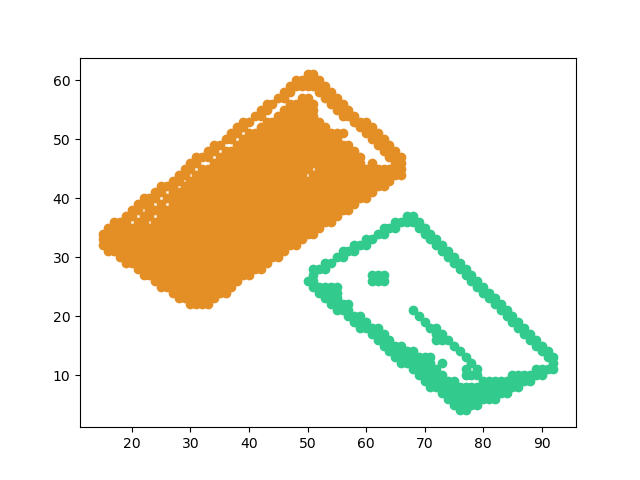
Figure1.png

笔记
#Python #算法
谱聚类再探
https://siegelion.cn/2020/03/20/谱聚类再探/
作者
siegelion
发布于
2020年3月20日
许可协议