编译原理笔记（3）

本文最后更新于 2024年6月7日下午

第三章

词素、词法单元、模式
- 词素：根据源程序的字符序列中与某个模式匹配的子序列，可以用正规集来理解。
- 词法单元：根据识别出的词素形成词法分析的输出，格式为
  
  <token-name , attribute-value>
- 模式:描述词素可能具有的形式，可以用正规式来理解。
词法分析器的作用
- 根据源程序输入的字符流，将他们组成词素，进而输出词法单元序列。
- 词法分析器一般是作为子程序供语法分析程序进行调用的,语法分析使用getNextToken函数调用词法分析，生成一个词法单元返回语法分析。
- 词法分析阶段还和符号表进行交互。
词法分析器的功能
- 识别单词（词素）
- 删除注释和空白
- 将错误信息与源程序的位置联系起来（词法分析器会记录换行符的个数，以便记录错误的位置）
词法分析器的两个过程
- 扫描过程——删除注释、将多个空白符变为一个
- 词法分析过程
词法单元的属性（attribute-value）
- 关键字，运算符，界符：一般为空
- 标识符、常量：符号表项的指针
词法单元的名字（token-name）
- 一般用整数编号来表示
扫描缓冲区
- 经过预处理后的字符序列要经过扫描后识别出词素，扫描的过程中需要将字符序列加载至扫描缓冲区中。但是无论多大长度的缓冲区都没法保证单词不会溢出。
- 这时需要将缓冲区分为两个半区，每个半区的长度为N，并规定每个单词的长度不大于N。
例如 :
- 首先读入第一个单词，长度为K（K<N）,读入后送往扫描器扫描。
- 同时继续读入，从K+1位置处继续写入字符，这个时候会遇到该半区的长度不足以保存单词的情况，这时就会将字符写入到第二个半区中，单词一定会在第二个半区内结束。
- 以此类推直到第二个半区也不足以容纳下单词，则将字符写入第一个半区。因为第一个半区中的数据已经经过处理，所以是无用的可以进行覆盖。
- 两个半区交替使用，作为扫描缓冲区。
- 如果少于N个字符在半区内，需要使用eof表示末尾。
超前搜索
- 因为读取某些字符串时但凭前缀是无法判断词素到底是什么的，比如break是关键字，但breakit是标识符，在读取到break时是无法判断该此法单元到底是什么的。这个时候就需要继续向后读取多个字符判断其含义了。
- 起点指示器：标记当前单词的开始字符
- 搜索指示器：不断向前搜索直到遇到某个字符可以帮助确定之前的单词，这是将指示器移至单词结尾。
状态转换图
- 有向图，结点表示状态用圆圈表示，边上的权表示接受字符可以发生状态的转移。
- 状态转换图，有一个起始状态，至少有一个终结状态。
- 状态转换图用来识别一定的字符串。

状态转换图的实现

分支：

switch getchar()
{
    case 1 :
        .....
    case 2 :
        .....
    .....
    case N :
        .....
}

循环

getchar()
while(......)
{
    getchar()
    ......
}
.......

终结

1	`return (code , value)`

code为识别出的单词的种类，value为单词的属性值或为空。
带*的终态结点，表示多接受了一个不属于当前单词的字符，必须把搜索指示器向前退回一个单位。

状态转换图的实现举例

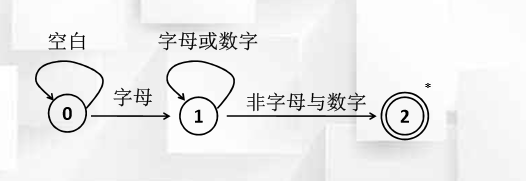
变量及方法
- strToken 存放单词的字符串
- code 词法单元类型（标识符为0）
- value 词法单元对应的符号表指针
- getBC( ) 跳过空白
- concat( ) 连接字符串
- reserve( ) 查找符号表
- retract( ) 回退指针
- insertId( ) 词法单元相关属性插入符号表
实现

init : strToken="";
getchar();
getBC();
if(isLetter()){
    while(isLetter() or isDigit()){
        concat();
        getchar();
    }
    retract();
    code=reserve();
    if(code == 0){
        value=insertId(strToken)
        return($ID , value)
    }
    else{
        return (code , )
    }
}
else{
    goto init;
}

正规式与正规集
- 正规式：
  - 空集ф与空字ε是正规式。
  - 字符集Σ中的每一个字符可以看作一个正规式。
  - 上面的正规式经过|、·、*有限次运算构成的式子也是正规式。（优先级：* > · > |）
- 正规集：正规式能表示的全体字符串的集合。

正规式的四则运算：

- U|V = V|U（交换律） 
- U|(V|W) = (U|V)|W (结合律) 
- U(VW) = (UV)W (结合律) 
- U(V|W) = UV|UW (分配律) 
- (V|W)U = VU|WU (分配律) 
- εU = Uε = U

有限自动机（FA）
- 有限自动机是词法分析的核心，可以用来识别正规集。
- 分为两类：DFA（确定）、NFA（不确定），DFA是NFA的一种特殊形式。
- FA M所能识别的字的全体记为 L(M)。
DFA
- 一个确定的有限自动机是M一个五元组：
  M = (S , Σ , δ , s0 , F)
  - S为状态集。
  - Σ为接受的字符集。（ε不属于Σ）
  - δ为映射函数。
  - s0为唯一的初始状态。
  - F为接收状态（终结状态）集合。（可空）
- 含有m个状态和n个输入字符
- 图含有m个状态结点，从1个结点出发，顶多有n条边和别的结点相连接，每条边用∑中的1个不同输入字符作标记
- 整张图含有唯一的1个初态结点
- 有若干个(可以是0个)终态结点
NFA
- NFA和DFA类似也是一个五元式，但而二者有不同之处。
- NFA的字符集Σ中包含ε
- NFA的初始状态可以不唯一
- NFA的同一状态接受同一字符可以转到多个状态
- NFA的边上可以是字
正规文法和有限自动机的等价性
- 左线性文法
  1. 新增一个开始状态结点S，文法的开始符号Z作为有限自动机的终结结点
  2. 形如 A -> Ba 画为
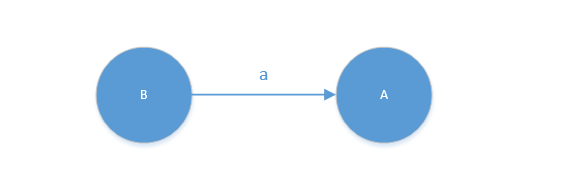
  3. 形如 A -> a 画为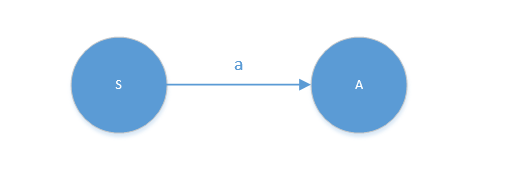
- 右线性文法
  1. 新增一个终结状态结点Z，文法的开始符号S作为有限自动机的开始结点
  2. 形如 A -> aB 画为
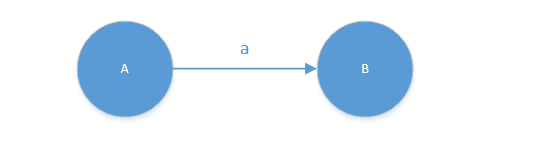
  3. 形如 A -> a 画为
正规式转化为确定化DFA
1. 根据正规式画出状态转化图（NFA）
2. 画出状态转换表
3. 根据状态转换表画出DFA
4. 将DFA确定化，得出最后确定的有限自动机