编译原理笔记(6)
本文最后更新于 2024年6月7日 下午

-
引入中间代码的作用
- 使编译程序在结构上更清晰(前端、后端)
- 便于进行代码优化
- 便于移植
-
后缀式
- 后缀式不使用括号,只要知道运算符的数目,无论是从左端还是右端扫描,都可以对齐进行无歧义的分解
-
表达式向后缀式的翻译

-
有向无环图(DAG)
- 内部结点代表运算符
- 公共表达式会有多个父节点(即该表达式参与了多个运算)
-
DAG的生成方式
- 首先画出产生式的语法树
- 对语法树的重复子树进行合并
-
三地址代码形式
x := y op z
-
四元式
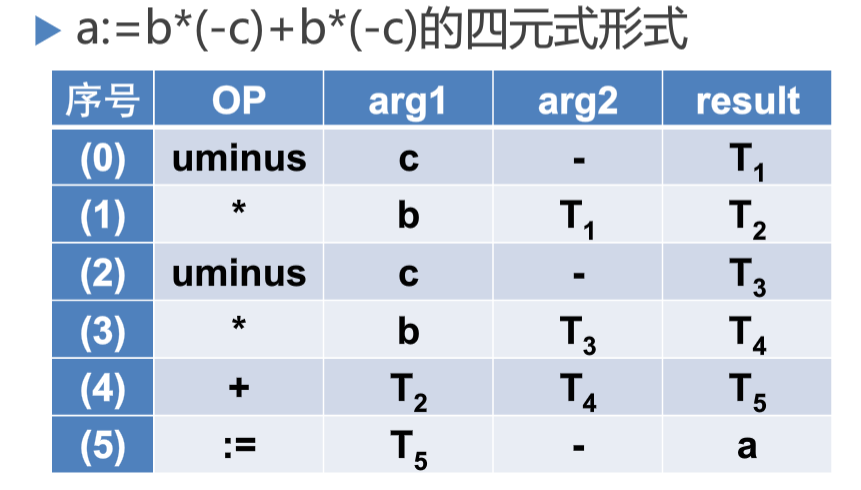
-
三元式
- 相比于三元式没有了
result域保存表达式的值,使用序号代表相应表达式的值
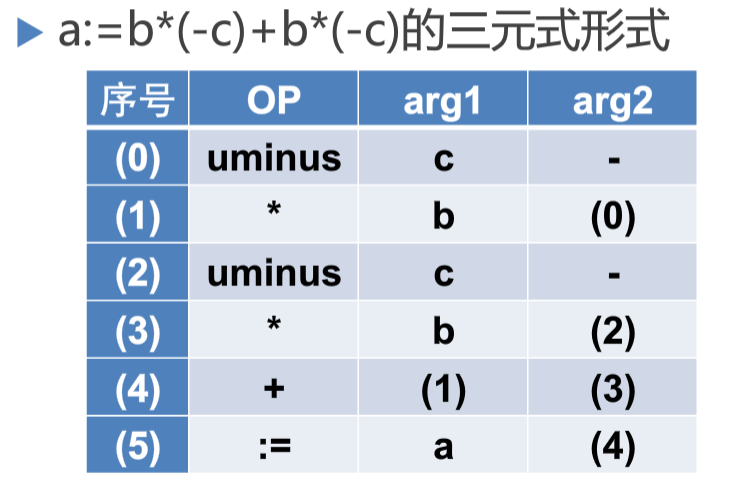
- 相比于三元式没有了
-
间接三元式
- 使用三元式+间接码表
- 解决了三元式中某些表达式需要反复计算的问题,并且优化起来很方便

-
翻译语句的属性文法 *
S.place表示存储非终结符S值的地址S.code表示对S值计算的三地址代码序列(后缀式)
-
赋值语句的三地址代码翻译模式 *

-
数组元素地址计算
- $ A [ i_1 , i_2 , i_3 , … , i_n ] = A + ((((i_1-low_1)*n_2+i_2-low_2)*n_3…)*n_k + i_k - low_k ) * w $
该表达式中 $ low_1 , low_2 ,…, low_n $ 是确定的所以可以对上面的式子进行一个分解
- $ A [ i_1 , i_2 , i_3 , … , i_n ] = offset + base - c $
- $ base = A $
- $ offset=(((i_1 * n_2 + i_2) * n_3 …) * n_k+ i_k) * w $
- $ c = (((low_1 * n_2 + low_2) * n_3…) * n_k+low_k) * w $
-
数组元素引用的翻译模式 *
-
将文法改写为
$ L \rightarrow Elist ] | id $
$ Elist \rightarrow Elist , E | id [E $ -
引入下列语义
- Elist.ndim:下标个数计数器
- Elist.place:保存数组Offset部分被计算出来的值
- Elist.array:数组名
- limit(array,j):给出数组第j维的长度
-
几个关键的产生式的语义
$ Elist \rightarrow id [ E$1
2
3
4Elist.place = E.place
Elist.ndim = 1
Elist.array = id.place$ Elist \rightarrow Elist ,E $
1
2
3
4
5
6
7
8t=newtemp
m=ndim+1
t=Elist.place*limit(Elist.array,m)
t=t+E.place
Elist.array=Elist.array
Elist.place=t
Elist.ndim=m$ L \rightarrow Elist ] $
1
2
3
4
5L.place=newtemp
L.offset=newtemp
L.place=Elist.array - C
L.offset=w*Elist.place
-
-
例题:A是一个二维数组,即n1=10,n2=20,w=4,数组的第一个元素为A[1,1],请给出
x:=A[y,z]的三代码语句序列。1
2
3
4
5
6t1 = y * 20
t2 = t1 + z
t3 = t2 * 4 # offset
t4 = A - ( 1 * 20 + 1 ) * 4 # base-c
t5 = t4[t2]
x = t5 -
例题:按照作为条件控制的布尔式翻译写出布尔式
A or (B and not (C or D))的四元式序列。1
2
3
4
5
6
7
8
9(1) ( jnz , A , _ , 0 )
(2) ( j , _ , _ , 3 )
(3) ( jnz , B , _ , 5 )
(4) ( j , _ , _ , 0 )
(5) ( or , C , D , T1)
(6) ( not , T1 , _ , T2)
(7) ( jnz , T2 , _ , 1 )
(8) ( j , _ , _ , 4 ) -
例题:把下面的语句翻译成四元式序列:
1 | |
1 | |
编译原理笔记(6)
https://siegelion.cn/2020/05/02/编译原理笔记(6)/