故障树分析(FTA)
本文最后更新于 2024年6月7日 下午
故障树分析,就是选择某一故障作为顶层事件,逐步拆解事件为中间事件,直到事件无法拆解变为底层事件。拆解事件的过程可以画成一棵树,这棵树也就称为故障树,利用故障树分析底层事件对故障发生影响的重要程度称为故障树分析。
建树符号
事件符号
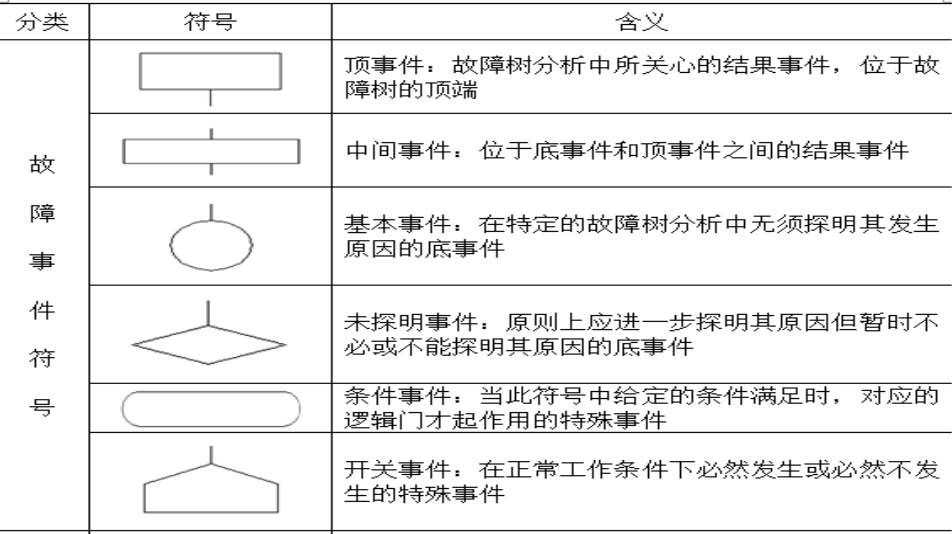
逻辑符号
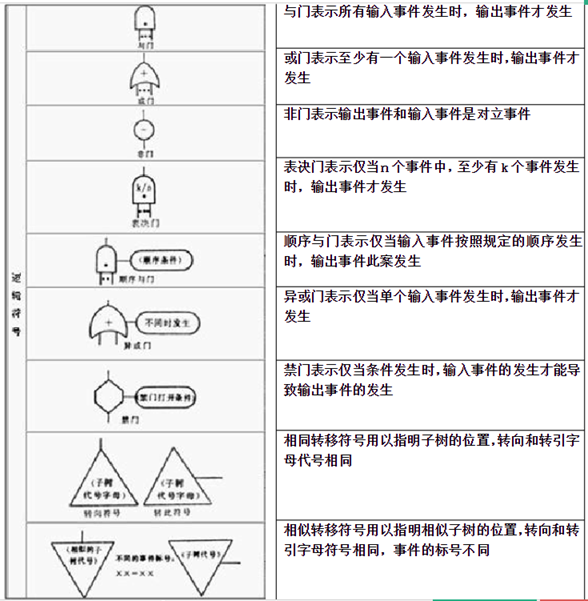
结构函数
-
底事件状态
1
2
3
4
5x_i=
\begin{cases}
0,故障\\
1,正常\\
\end{cases} -
顶事件状态
可用与底事件有关的函数表示
1
2
3
4
5
6
7T=\phi(x_1,x_2...x_n)
\phi(T)=
\begin{cases}
0,故障\\
1,正常\\
\end{cases} -
计算
- 或门
1
\phi(T)=\sum_{i=1}^{n}{x_i}- 与门
1
\phi(T)=\prod_{i=1}^{n}{x_i} -
化简
1
T=x_1(x_1+x_4)x_3=x_1x_3+x_1x_4x_3=x_1x_3 -
最小割集
- 最小割集是指,是指让顶层事件发生的最少数量的底层事件集合
- 例:
- 顶层事件T可以表示为
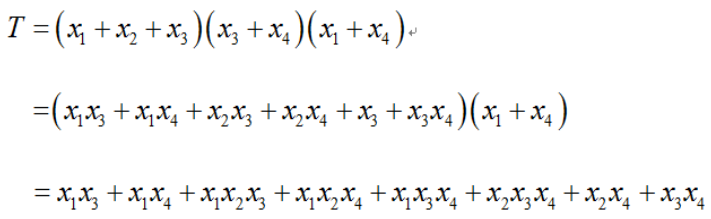
- 化简为
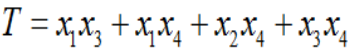
- 根据表达式为或运算,则可知有4个最小割集,为:
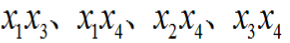
- 顶层事件T可以表示为
-
路集
- 是割集的对偶集合,也即不触发发生顶层事件的底层事件集合
顶层事件概率的计算
- 将顶层事件表示为,最小割集的形式
1
T=\phi(x_1,x_2...x_n) - P为计算事件的概率,则
1
P(T)=\phi(P(x_1),P(x_2)...P(x_n))
结构重要度计算
- 设顶层事件T,底层事件共n个
- 计算底层事件x发生的情况下,顶层事件T发生的情况共p个
- 计算底层事件x不发生的情况下,顶层事件T发生的情况共q个
- 则事件x的结构重要度为
1
I(x)=\frac{1}{2^{n-1}} [p-q]
概率重要度计算
- 列出所有底事件状态组合与对应的顶事件状态
- 找到其中其他条件相同,底事件x取1时顶事件T为1,底事件x取0顶事件T为0的情况。
- 计算概率
- 例:
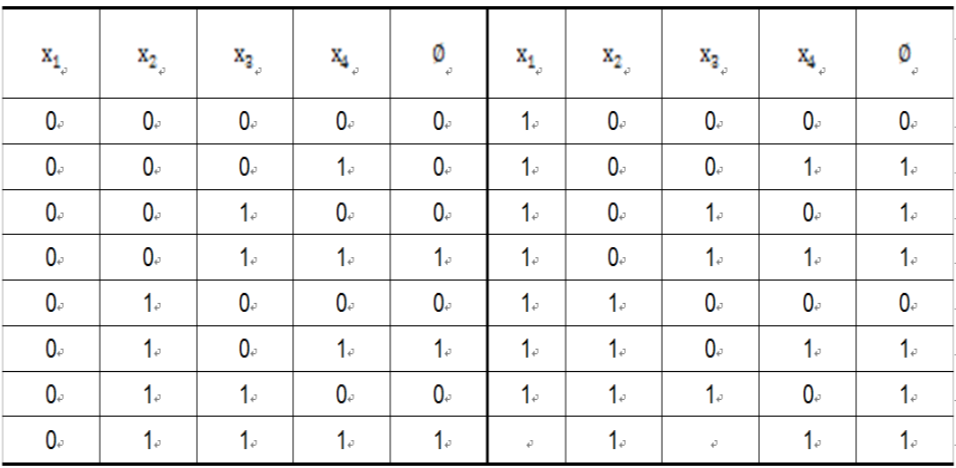
- 组合1001、1010、1110满足条件
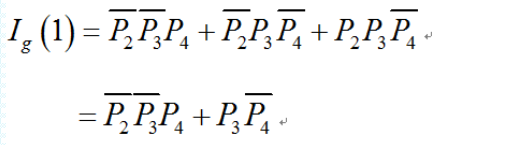
关键重要度计算
1 | |
故障树分析(FTA)
https://siegelion.cn/2020/05/22/故障树分析(FTA)/