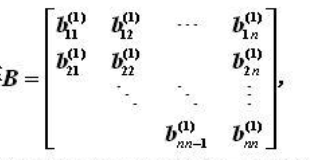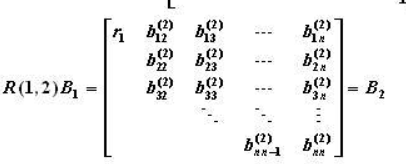利用Hadoop平台实现分布式谱聚类算法思路

传统谱聚类算法实现步骤

1. 构建邻接矩阵W
2. 计算度矩阵 D
3. 计算拉普拉斯矩阵矩阵 L
4. 计算L的特征向量，k个最小的特征值对应的特征向量对应的特征向量组成矩阵Z
5. 标准化Z
6. 使用 K-mean 进行最后的聚类

并行谱聚类算法

引入并行的目的

为何要将传统的分布式算法改进为并行的分布式谱聚类算法呢？目得无外乎提升聚类速度与解决矩阵过大无法一次性载入内存。

所以我们追求的目标为：尽量使矩阵成为稀疏矩阵，这样既节省存储空间又利于加速聚类。

构造邻接矩阵

以往使用全连接法，每个节点之间都需要计算距离这显然是不符合我们的要求的。故此次我们采用“ε近邻法”构造进阶矩阵。

---

伪代码：

节点作为全局变量存在HBase中，最后构造出的邻接矩阵也存于HBase中

input : <key,null>
ouput : <key,null>
index = key 
anotherIndex = n-key+1

for i in [index,anotherIndex]:
    i_node_data = getNodeData(i)
    for j in range(i,n):
        j_node_data = getNodeData(j)
        sim=computeSimilarity(i_node_data,j_node_data)
        if sim < ε:
            storeW(i,j,sim)
            storeW(j,i,sim)
        else:
            storeW(i,j,0)
            storeW(j,i,0
        endif
    endfor
endfor

output<key,null>

可以看到，每次我们进行计算时，计算的是节点i与节点i、i+1、…、n节点之间的相似度。也就是说节点1需要计算n次，但节点n只需要计算1次，所以为了平衡每台机器上的计算量，将节点i与n-i+1的计算分配到同一台机器上。

计算度矩阵与拉普拉斯矩阵

伪代码：

****Map函数****

input : <key,value> (key为行号，value为邻接矩阵第key行对应的向量)

ouput : <key,value>(key为行号，value为该行元素求和)

index = key
for i in range(1,n):
    sum += value[i]
endfor

storeD(index,index,sum)

output<key,sum>

****Reduce函数****

input : <key,value> 
ouput : <key,null>

index = key

metrix=getWData(index)

for i in range(1,n):
    if i==index:
        storeL(index,i,value-metrix[index][i])
    else:
        storeL(index,i,metrix[index][i])
endfor

output<key,null>

计算特征向量

难点

1. 利用Lanczos算法将拉普拉斯矩阵转换为对三角矩阵

Lanczos 算法

Lanczos算法认为若A为对称矩阵，则存在一个正交矩阵 $Q_n$，使得$T_n=Q_n^TAQ_n$成立，其中$T_n$为对三角矩阵

如何求出$T_n$呢？
$$
Q_n^TAQ_n=T_n \Rightarrow AQ_n=Q_nT_n
$$

$$
Q_n=(q_1,q_2,…q_n)
$$

则

$$
Aq_n=q_{n-1}b_{n-1}+q_na_n+q_{n+1}b_{n}
$$

$$
q_{n+1}b_n=r=Aq_n-q_{n-1}b_{n-1}+q_na_n
$$
$$
a_n=q_n^TAq_n
$$
$$
b_n=||r||_2
$$

可令

$$
||q_1||_2=1
$$

进行迭代

$$
q_0b_0=q_{n+1}b_{n+1}=0
$$

$$
a_n=q_n^TAq_n
$$

$$
r=Aq_n-q_{n-1}b_{n-1}+q_na_n
$$

$$
b_n=||r||_2
$$

$$
q_{n+1}=r/b_n
$$

$$
a_{n+1}=q_{n+1}^TAq_{n+1}
$$

迭代停止条件为$b_n=0$

2. 利用QR算法不断迭代，逐步逼近矩阵的特征值

QR分解

算法的主要思想为：A=QR这一过程将矩阵分解为Q和R两部分，其中Q是标准正交矩阵，R是一个上三角矩阵。主要的分解算法有多种，这里对Given方法与Gram-Schmidt方法加以说明。

Given

对于一个给定的hessnberg矩阵

构造一个矩阵

其中

$$
cos\theta=b_{11}^{(1)}/r
$$

$$
sin\theta=b_{21}^{(1)}/r
$$

$$
r=\sqrt{ {b_{11}^{ (1) } }^2 + {b_{21}^{ (1) } }^2}
$$

相乘得

继续构造

最终对角线的左下角的元素全部清零

此时有公式成立

$$
B=QR
$$

$$
Q=R(2,1)^T * R(3,2)^T * … * R(n+1,n)^T
$$

令

$$
B=RQ
$$

开始新一轮迭代，重复数轮，最终矩阵B对角线上上的元素值即为原矩阵特征值。

---

下为迭代一次的Python代码，来自vonZooming的回答

def givens_reduce(matrix_a):
    """
    Givens reduce for QR factorization.
    :param matrix_a:
    :return: matrix_q, matrix,r

    Parameters:
    -----------
    matrix_a: np.ndarray
        original matrix to be Givens Reduce factorized.

    """

    # row num: n
    # col num: m
    n, m = matrix_a.shape

    matrix_r = matrix_a

    # R_1, R_2, ... R_n
    givens_matrix_list = []

    # Rotation each entry in matrix
    for j in range(m):  # Col-m
        for i in range(j+1, n):  # Row-n

            if matrix_r[i][j] == 0:
                continue

            """ Find a and b (current entry) """
            a = matrix_r[j][j]
            b = matrix_r[i][j]

            # Prepare c and s
            base = np.sqrt(np.power(a, 2) + np.power(b, 2))
            c = np.true_divide(a, base)
            s = np.true_divide(b, base)

            # Givens trans matrix
            matrix_g = np.identity(n)

            matrix_g[j][j] = c  # Upper Left
            matrix_g[i][j] = -s  # Lower Left

            matrix_g[j][i] = s  # Upper Right
            matrix_g[i][i] = c  # Lower Right

            # Rotation
            matrix_r = np.matmul(matrix_g, matrix_r)

            givens_matrix_list.append(matrix_g)

    """ Reduce R matrix """
    matrix_r = matrix_r[0: m]

    # Compute Q', where Q' = Rn...R2*R1*A
    matrix_q = np.identity(n)
    for givens_matrix in givens_matrix_list:
        matrix_q = np.matmul(givens_matrix, matrix_q)

    # Get Q
    matrix_q = np.transpose(matrix_q[0: m])

    return matrix_q, matrix_r

Gram-Schmidt

详细方法可以参照论文《QR Decomposition with Gram-Schmidt》

3. 利用特征值反推特征向量

并行化K-mean算法